Alt-Ergo Overview
In this preliminary chapter, we’ll have a look at Alt-Ergo. What is it ? What is it good for ? How does it interact with other tools ?
What is it ?
Automatic theorem prover
Alt-Ergo is an automatic theorem prover (ATP), specially designed to prove properties about programs, such as their correctness.
Unlike interactive theorem provers (ITP) – such as Coq, Agda, Isabelle and HOL – Alt-Ergo proves formulas by itself. Just Ask Alt-Ergo !
ATP are great at solving relatively simple problems, but some may still require human assistance. Tools such as Why3 make it possible to use ATP along with ITP.
A native language designed for program verification
Alt-Ergo’s native language is especially convenient for reasoning about computer programs.
Polymorphism and algebraic datatypes makes it easy to model various data structures.
It is human-readable, unlike most other languages for SMT-solvers.
Note that Alt-Ergo supports other input languages, such as SMT-LIB, the standard input language for SMT-solvers.
SMT-solver
More specifically, Alt-Ergo is an SMT-solver. Solvers of this family have made impressive advances and became very popular during the last decade. They are now used is various domains such as hardware design, software verification and formal testing.
The Satisfiability Modulo Theory (SMT) problem is a decision problem.
SMT decision problem
- Input
A formula in first order logic
A theory: additional axioms which provide an interpretation for some symbols
- Output
Is the formula satisfiable (SAT) or unsatisfiable (UNSAT) ?
In other words, is it possible to find an interpretation of all symbols that makes the formula true while being compatible with the theory ?
As Alt-Ergo is specialized in theorems about programs, it actually states the problem in a slightly different way.
SMT decision problem in Alt-Ergo
- Input
A formula in first order logic
A theory: additional axioms which provide an interpretation for some symbols
- Output
Is the formula Valid or Invalid ?
In other words, is the formula true for all theory-compatible interpretations of the symbols ?
Note
Those two problems are actually the same: you can switch from one to the other by negating the formula !
A couple of things should be noted to give a better understanding of the problem.
Warning
Undecidability
This general version of the SMT problem is undecidable: it is impossible to write a program that will always answer Valid or Invalid in a finite time, and always give the correct answer !
Principle of explosion
If incompatible assumptions are made in the theory, no interpretation will be compatible with the theory. Therefore, all formulas will be Valid !
Because of this, Alt-Ergo can have other answers than Valid and Invalid.
Answer |
Meaning |
|---|---|
Valid |
The formula has been proven correct: all interpretations compatible with the axioms make the formula true. |
I don’t know |
The formula may or may not be valid. |
Inconsistent assumption |
An inconsistency has been detected in the theory ! |
Invalid |
There exists an interpretation which falsifies the formula. |
Note that as Alt-Ergo focuses on proving that programs are correct, the last case doesn’t currently happen: Alt-Ergo will answer I don’t know rather than Invalid.
In other words, Alt-Ergo deals with UNSAT, not SAT.
Some experimental support exists for the generation of counter-examples (models) which falsifies the formula. This will be expanded in future versions.
Reasoners for several theories
Note that this undecidability depends on the axioms being used. For several interesting theories, the problem is actually decidable.
Alt-Ergo has built-in support for a number of interesting theories, relevant to computer programs.
The free theory of equality with uninterpreted symbols
Associative and commutative (AC) symbols
Linear arithmetic over integers and rationals
(Fragment of) non-linear arithmetic
Floating-point arithmetic (as an extension)
Enumerated datatypes
Record datatypes
Polymorphic functional arrays
Fixed-size bitvectors
Creating reasoners for a combination of theories is a difficult problem, even when a reasoner is known for each of these theories taken separately.
Alt-Ergo handles this issue through a combination of Shostak-like and Nelson-Oppen like approaches.
Thanks to this, Alt-Ergo is great at reasoning on real-life problems, which often mix several theories.
How does it relate to other tools ?
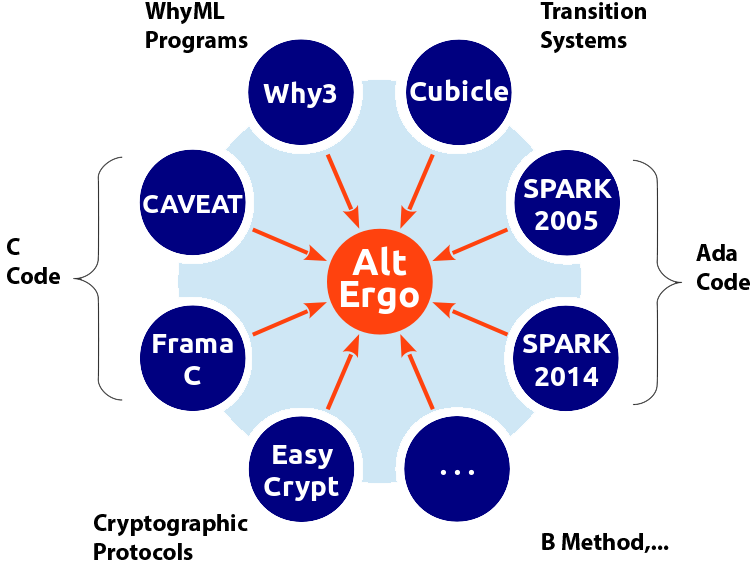
Alt-Ergo is very successful for proving formulas generated in the context of deductive program verification. It was originally designed and tuned to be used by the Why platform. Currently, it is used as a back-end of different tools and in various settings, in particular via the Why3 platform. For instance, the Frama-C suite relies on it to prove formulas generated from C code, and the SPARK toolset uses it to check formulas produced from Ada programs. In addition, Alt-Ergo is used to prove formulas issued from B modelizations and from cryptographic protocols verification. The figure given below shows the main tools that rely on Alt-Ergo to prove the formulas they generate.