Appendix: Experimental support for models and counter-examples generation
Alt-Ergo is specialized in program verification, and thus focuses on proving that formulas are Valid (UNSAT).
However, even in the context of program verification, it may be useful to build counter-examples, explaining to the programmer why the formulas are Invalid.
In the context of SAT (Invalid being its negative formulation) this can be interpreted as the construction of a model for each formula which is satisfiable.
Alt-Ergo’s support for models and counter-examples is still experimental, but should be extended in future versions.
Options for model generation
Two options are available to create models/counter-examples.
When alt-ergo is used in command line, they correspond to --model and --interpretation.
Their maximum level are respectively --model=complete and --interpretation = 3.
Using them, here is the kind of output you could get.
Example: No model generation
logic x, y: int
goal g:not(
x+y = 8 and
x*y = 12
)
Example: Using model = complete
logic x, y: int
goal g:not(
x+y = 8 and
x*y = 12
)
Example: Using interpretation = 3
logic x, y: int
goal g:not(
x+y = 8 and
x*y = 12
)
Examples
All of the code boxes below have been set up with interpretation = 3.
Simple equations
Model generation can be used to solve simple equations.
All four examples below come from the fun book “SAT/SMT by example” by Dennis Yurichev.
Don’t hesitate to check his book for more fun applications of SMT-solvers, such as cracking programs using rand, solving nonograms, checking hacks from Henry Warren’s “Hacker’s delight”, or superoptimization.
School-level system of equation
This comes from Yurichev’s 2.2.1, copy pasted from this wikipedia page.
The following code solves this simple system of equations.
logic x,y,z:real
goal system: not(
3.*x+2. *y- z = 1. and
2.*x-2. *y+4.*z = -2. and
-x+ .5*y+ z = 0.
)
Another school-level system of equations
This comes from Yurichev’s 2.2.2, and was apparently found “somewhere on Facebook”.
The following code solves this system.
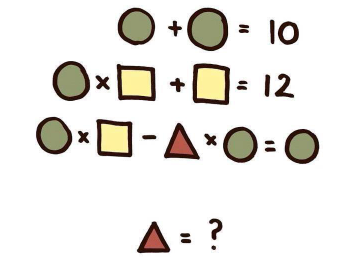
logic circle, square, triangle: int
goal system: not(
circle + circle = 10 and
circle*square + square = 12 and
circle*square - triangle*circle = circle
)
XKCD 287
This comes from Yurichev’s 3.1, inspired by xkcd 287.
logic a,b,c,d,e,f:int
axiom positive:
a>=0 and b>=0 and c>=0 and d>=0 and e>=0 and f>=0
goal system: not(
215*a+275*b+335*c+355*d+420*e+580*f=1505
(* Uncomment to find another solution *)
(* and not(a=7 and b=0 and c=0 and d=0 and e=0 and f=0) *)
(* Valid if next line uncommented *)
(* and not(a=1 and b=0 and c=0 and d=2 and e=0 and f=1 *)
)
Art of Problem Solving
This comes from Yurichev’s 3.6, inspired by this problem from the Art of Problem Solving.
The sum of two nonzero real numbers is 4 times their product.
What is the sum of the reciprocals of the two numbers?
logic x,y:real
logic res:real
axiom positive:
x>0. and y>0.
axiom result:
res = 1./x + 1./y
goal g:not(
x+y = 4.*x*y
)
Other examples
Primality tester
Strangely enough, Alt-Ergo seems to prove that \(57\), “Grothendieck’s prime”, is not actually prime.
logic a,b,n:int
axiom init: n=57
axiom range: 1<=a<=n and 1<=b<=n
goal is_prime:
a*b = n ->
a=1 or b=1
Sudoku solver 4*4
This solves the following sudoku puzzle.
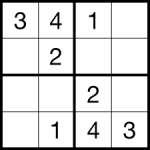
type one_four = One | Two | Three | Four
logic grid: int, int -> one_four
predicate by_row =
forall i:int. 0<=i<4 ->
distinct(grid(i,0),grid(i,1),grid(i,2),grid(i,3))
predicate by_column =
forall j:int. 0<=j<4 ->
distinct(grid(0,j),grid(1,j),grid(2,j),grid(3,j))
predicate by_square =
forall i,j:int. 0<=i<2 -> 0<=j<2 ->
distinct(grid(2*i,2*j),grid(2*i,2*j+1),grid(2*i+1,2*j),grid(2*i+1,2*j+1))
axiom init:
grid(0,0)=Three and grid(0,1)=Four and grid(0,2)=One and
grid(1,1)=Two and
grid(2,2)=Two and
grid(3,1)=One and grid(3,2)=Four and grid(3,3)=Three
goal g: not
(by_row and by_column and by_square)
Sudoku solver 9*9
The following sudoku puzzle has been designed by the Finnish mathematician Arto Inkala, and has been coined “the world’s hardest sudoku” by several newspapers.
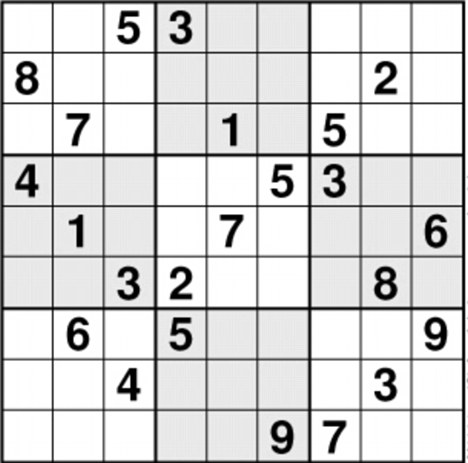
Using the following code, Alt-Ergo solves it in about 30 000 steps, which is ~ \(2\) seconds on a cheap personal computer (not with the in-browser version).
type one_nine = One | Two | Three
| Four | Five | Six
| Seven | Eight | Nine
logic grid: int, int -> one_nine
predicate by_row =
distinct(grid(0,0),grid(0,1),grid(0,2),
grid(0,3),grid(0,4),grid(0,5),
grid(0,6),grid(0,7),grid(0,8)) and
distinct(grid(1,0),grid(1,1),grid(1,2),
grid(1,3),grid(1,4),grid(1,5),
grid(1,6),grid(1,7),grid(1,8)) and
distinct(grid(2,0),grid(2,1),grid(2,2),
grid(2,3),grid(2,4),grid(2,5),
grid(2,6),grid(2,7),grid(2,8)) and
distinct(grid(3,0),grid(3,1),grid(3,2),
grid(3,3),grid(3,4),grid(3,5),
grid(3,6),grid(3,7),grid(3,8)) and
distinct(grid(4,0),grid(4,1),grid(4,2),
grid(4,3),grid(4,4),grid(4,5),
grid(4,6),grid(4,7),grid(4,8)) and
distinct(grid(5,0),grid(5,1),grid(5,2),
grid(5,3),grid(5,4),grid(5,5),
grid(5,6),grid(5,7),grid(5,8)) and
distinct(grid(6,0),grid(6,1),grid(6,2),
grid(6,3),grid(6,4),grid(6,5),
grid(6,6),grid(6,7),grid(6,8)) and
distinct(grid(7,0),grid(7,1),grid(7,2),
grid(7,3),grid(7,4),grid(7,5),
grid(7,6),grid(7,7),grid(7,8)) and
distinct(grid(8,0),grid(8,1),grid(8,2),
grid(8,3),grid(8,4),grid(8,5),
grid(8,6),grid(8,7),grid(8,8))
predicate by_column =
distinct(grid(0,0),grid(1,0),grid(2,0),
grid(3,0),grid(4,0),grid(5,0),
grid(6,0),grid(7,0),grid(8,0)) and
distinct(grid(0,1),grid(1,1),grid(2,1),
grid(3,1),grid(4,1),grid(5,1),
grid(6,1),grid(7,1),grid(8,1)) and
distinct(grid(0,2),grid(1,2),grid(2,2),
grid(3,2),grid(4,2),grid(5,2),
grid(6,2),grid(7,2),grid(8,2)) and
distinct(grid(0,3),grid(1,3),grid(2,3),
grid(3,3),grid(4,3),grid(5,3),
grid(6,3),grid(7,3),grid(8,3)) and
distinct(grid(0,4),grid(1,4),grid(2,4),
grid(3,4),grid(4,4),grid(5,4),
grid(6,4),grid(7,4),grid(8,4)) and
distinct(grid(0,5),grid(1,5),grid(2,5),
grid(3,5),grid(4,5),grid(5,5),
grid(6,5),grid(7,5),grid(8,5)) and
distinct(grid(0,6),grid(1,6),grid(2,6),
grid(3,6),grid(4,6),grid(5,6),
grid(6,6),grid(7,6),grid(8,6)) and
distinct(grid(0,7),grid(1,7),grid(2,7),
grid(3,7),grid(4,7),grid(5,7),
grid(6,7),grid(7,7),grid(8,7)) and
distinct(grid(0,8),grid(1,8),grid(2,8),
grid(3,8),grid(4,8),grid(5,8),
grid(6,8),grid(7,8),grid(8,8))
predicate by_square =
distinct(grid(0,0),grid(0,1),grid(0,2),
grid(1,0),grid(1,1),grid(1,2),
grid(2,0),grid(2,1),grid(2,2)) and
distinct(grid(0,3),grid(0,4),grid(0,5),
grid(1,3),grid(1,4),grid(1,5),
grid(2,3),grid(2,4),grid(2,5)) and
distinct(grid(0,6),grid(0,7),grid(0,8),
grid(1,6),grid(1,7),grid(1,8),
grid(2,6),grid(2,7),grid(2,8)) and
distinct(grid(3,0),grid(3,1),grid(3,2),
grid(4,0),grid(4,1),grid(4,2),
grid(5,0),grid(5,1),grid(5,2)) and
distinct(grid(3,3),grid(3,4),grid(3,5),
grid(4,3),grid(4,4),grid(4,5),
grid(5,3),grid(5,4),grid(5,5)) and
distinct(grid(3,6),grid(3,7),grid(3,8),
grid(4,6),grid(4,7),grid(4,8),
grid(5,6),grid(5,7),grid(5,8)) and
distinct(grid(6,0),grid(6,1),grid(6,2),
grid(7,0),grid(7,1),grid(7,2),
grid(8,0),grid(8,1),grid(8,2)) and
distinct(grid(6,3),grid(6,4),grid(6,5),
grid(7,3),grid(7,4),grid(7,5),
grid(8,3),grid(8,4),grid(8,5)) and
distinct(grid(6,6),grid(6,7),grid(6,8),
grid(7,6),grid(7,7),grid(7,8),
grid(8,6),grid(8,7),grid(8,8))
axiom init:
grid(0,0)=Eight and grid(1,2)=Three and grid(2,1)=Seven and
grid(1,3)=Six and grid(2,4)=Nine and
grid(2,6)=Two and
grid(3,2)=Five and
grid(3,5)=Seven and grid(4,4)=Four and grid(4,5)=Five and grid(5,3)=One and
grid(4,6)=Seven and grid(5,7)=Three and
grid(6,2)=One and grid(7,2)=Eight and grid(8,1)=Nine and
grid(7,3)=Five and
grid(6,7)=Six and grid(6,8)=Eight and grid(7,7)=One and grid(8,6)=Four
goal g: not
(by_row and by_column and by_square)
The output provided by Alt-Ergo is
( (by_row FT:[by_row]) (by_column FT:[by_row]) (by_square FT:[by_row])
((grid 8 6) X5(Sum):[Four])
((grid 6 0) X5(Sum):[Four])
((grid 7 5) X5(Sum):[Four])
((grid 3 7) X5(Sum):[Four])
((grid 1 8) X5(Sum):[Four])
((grid 2 3) X5(Sum):[Four])
((grid 5 1) X5(Sum):[Four])
((grid 4 4) X5(Sum):[Four])
((grid 0 2) X5(Sum):[Four])
((grid 8 4) X5(Sum):[One])
((grid 6 2) X5(Sum):[One])
((grid 7 7) X5(Sum):[One])
((grid 3 8) X5(Sum):[One])
((grid 1 6) X5(Sum):[One])
((grid 2 5) X5(Sum):[One])
((grid 5 3) X5(Sum):[One])
((grid 4 0) X5(Sum):[One])
((grid 0 1) X5(Sum):[One])
((grid 8 3) X5(Sum):[Eight])
((grid 6 8) X5(Sum):[Eight])
((grid 7 2) X5(Sum):[Eight])
((grid 3 6) X5(Sum):[Eight])
((grid 1 5) X5(Sum):[Eight])
((grid 2 7) X5(Sum):[Eight])
((grid 5 4) X5(Sum):[Eight])
((grid 4 1) X5(Sum):[Eight])
((grid 0 0) X5(Sum):[Eight])
((grid 8 5) X5(Sum):[Six])
((grid 6 7) X5(Sum):[Six])
((grid 7 1) X5(Sum):[Six])
((grid 3 4) X5(Sum):[Six])
((grid 1 3) X5(Sum):[Six])
((grid 2 2) X5(Sum):[Six])
((grid 5 0) X5(Sum):[Six])
((grid 4 8) X5(Sum):[Six])
((grid 0 6) X5(Sum):[Six])
((grid 8 7) X5(Sum):[Five])
((grid 6 1) X5(Sum):[Five])
((grid 7 3) X5(Sum):[Five])
((grid 3 2) X5(Sum):[Five])
((grid 1 4) X5(Sum):[Five])
((grid 2 0) X5(Sum):[Five])
((grid 5 6) X5(Sum):[Five])
((grid 4 5) X5(Sum):[Five])
((grid 0 8) X5(Sum):[Five])
((grid 8 1) X5(Sum):[Nine])
((grid 6 5) X5(Sum):[Nine])
((grid 7 6) X5(Sum):[Nine])
((grid 3 3) X5(Sum):[Nine])
((grid 1 0) X5(Sum):[Nine])
((grid 2 4) X5(Sum):[Nine])
((grid 5 8) X5(Sum):[Nine])
((grid 4 2) X5(Sum):[Nine])
((grid 0 7) X5(Sum):[Nine])
((grid 8 0) X5(Sum):[Three])
((grid 6 6) X5(Sum):[Three])
((grid 7 4) X5(Sum):[Three])
((grid 3 1) X5(Sum):[Three])
((grid 1 2) X5(Sum):[Three])
((grid 2 8) X5(Sum):[Three])
((grid 5 7) X5(Sum):[Three])
((grid 4 3) X5(Sum):[Three])
((grid 0 5) X5(Sum):[Three])
((grid 8 8) X5(Sum):[Seven])
((grid 6 4) X5(Sum):[Seven])
((grid 7 0) X5(Sum):[Seven])
((grid 3 5) X5(Sum):[Seven])
((grid 1 7) X5(Sum):[Seven])
((grid 2 1) X5(Sum):[Seven])
((grid 5 2) X5(Sum):[Seven])
((grid 4 6) X5(Sum):[Seven])
((grid 0 3) X5(Sum):[Seven])
((grid 8 2) X5(Sum):[Two])
((grid 6 3) X5(Sum):[Two])
((grid 7 8) X5(Sum):[Two])
((grid 3 0) X5(Sum):[Two])
((grid 1 1) X5(Sum):[Two])
((grid 2 6) X5(Sum):[Two])
((grid 5 5) X5(Sum):[Two])
((grid 4 7) X5(Sum):[Two])
((grid 0 4) X5(Sum):[Two])
)
File "", line 105, characters 9-53:
I don't know (1.9514) (30079 steps) (goal g)